凸优化的重要方法论_皇马娱乐建站工程集团

凸优化的重要方法论

发布时间：2024-04-07

阅读量：

字号：

优化方法是几乎所有机器学习模型中最重要的核心部分，其重要性也是需要强调的。凸优化是优化方法论中的特例，是一个非常大的领域，想要细致的学习需要花费不少时间，本文作为阶段性学习的总结，通过算法思维和常见算法的目标函数引出凸优化内容，并介绍了作为算法工程师我们最需要了解的凸优化领域的重要方法论，希望通过分享给大家，能够对大家在算法领域的学习有所帮助，如果本文中的方法论有误的话，还请各路大神进行指正。

算法思维及常见目标函数
凸集与凸函数
经典凸优化问题
非凸优化问题的优化

算法思维

针对一个AI问题，我们都可以将AI问题拆解为建立模型+优化模型这两块内容的，对于任何一个AI问题，其目标函数都可以用以下形式表示：

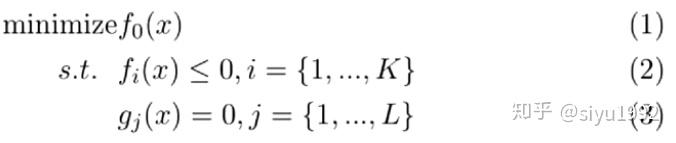
我将解决业务问题中的常用套路称为算法思维，并总结了以下4个重要步骤：

将业务场景中需要解决的问题转化为数学问题，并写出严格的数学模型（目标函数）
针对写出的数学模型判断凹凸性
根据目标的函数的凹凸性判断问题类型（如果目标函数是凸函数，我们需要判断该函数所属问题类型，常见的问题类型有Linear Programming、Quadratic Programming等；如果目标函数是非凸函数，也需要判断其所属问题类型，常见有Setcover Problem，Max flow Problem等）
根据不同的问题类型使用不同的优化方法论解决问题。

其实在实际解决问题的过程中，其实大家都不太会在意第1,2个步骤点，可能都会直接通过经验去查找相应的工具解决问题，但是这样的解决思路是不太好的，因为在这个过程中，我们可能不知道需要解决的问题和我们选择的工具是否匹配，如果结果不太理想，我们可能也不知道其中的原因。但是如果我们在解决问题前，定义了严格的目标函数，我们不仅可以针对该目标函数选择相应的优化方法，也可以根据业务场景，对目标函数进行相应调整，增加项目的成功率。

常见目标函数

我将工作中可能会用到的常见的一些算法的目标函数进行了列举，如下：

线性回归： $minimize_{w}||Xw - y||^{2}$
SVM： $minimize_{w}||w||^{2}+C\\sum_{i=1}^{n}{\\xi_{i}},s.t. \\xi_{i}\\geq1-y_{i}x_{i}^{T}w,\\xi_{i}\\geq0$
逻辑回归（二分类）： $minimize_{w,b}-\\sum_{i=1}^{n}ylog P(y=1|x,{w,b})+(1-y)log(1-P(y=1|x,{w,b}))$
协同过滤： $minmize_{w}\\sum_{i,j}^{}{log(1+exp(w^{T}x_{i}-w^{T}x_{j}))}$
K-means： $minimize_{\\mu_{1},...\\mu_{k}}J(\\mu)=\\sum_{j=1}^{k}\\sum_{i\\epsilon C_{j}}^{b}{||x_{i}-\\mu_{j}||^{2}}$

凸优化的重要性

从函数的凹凸性而言，我们通常把函数分为凸函数和非凸函数。凸函数是有且只有全局最优解的，而非凸函数可能有多个局部最优解，这些特性我会在下文中进行详细解释。在前言中，我提到过优化问题是机器学习模型中的核心部分，而针对不同模型，有不同的方法论对其目标函数进行优化。例如针对逻辑回归、线性回归这样的凸函数，使用梯度下降或者牛顿法可以求出参数的全局最优解，针对神经网络这样的非凸函数，我们可能会找到许多局部最优解。不难看出，我们希望在实际解决问题过程中，都希望我们建立的目标函数是凸函数，这样我们不必担心局部最优解问题，但实际上，我们遇到的问题大多数情况下建立的目标函数都是非凸函数，因此我们需要根据场景选择不同的优化方法。

凸优化定义

就定义而言，凸优化是：在最小化（最大化）的优化要求下，目标函数是凸函数且约束条件所形成的可行域集合是一个凸集的优化方法，因此凸优化的判定条件有两个，1.函数定义域是凸集 2.目标函数是凸函数。

凸集

凸集的定义：假设对于任意x, y ∈ C and 任意参数α ∈[0, 1], 我们有αx + (1 ? α)y ∈ C,集合C为凸集。

凸集的理解：对凸集的理解，我们可以分别从理论定义的角度和函数图像的角度两方面理解。从定义上讲，对于集合C中的任意两个元素x和y，需要满足αx + (1 ? α)y 的值也需要在集合C中；从函数图像角度讲，这个定义中的式子含义是，x、y两点连线上的任意一个点都需要属于集合C，如下图所示，任何证明集合是凸集的方法都可以通过定义和函数图像两方面进行。

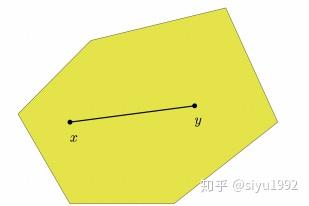
凸集的性质：两个凸集的交集也是凸集。

常见凸集与证明方法：

实数集合 $R^{n}$ （通过凸集的定义证明）
正数集合 $R_{+}^{n}$ （通过凸集的定义证明）
范数 $||x||\\leq1$ （通过凸集的定义证明：对于范数集合中的两点x和y，满足 $||x||\\leq1$ 、 $||y||\\leq1$ ，需证明 $||\\alpha x+(1-\\alpha)y||\\leq1$ 。由绝对值性质可将不等式左边的式子转换为 $||\\alpha x+(1-\\alpha)y||=||\\alpha x||+||(1-\\alpha)y||=\\alpha|| x||+(1-\\alpha)||y||\\leq1$ ）
线性方程的所有解Ax=b（通过凸集的定义证明：对于线性方程的两个点x和y，Ax=b、Ay=b，需证明 $A(\\alpha x+(1-\\alpha)y)=b$ ，通过对等式左边式子的变换，可得以下式子： $A(\\alpha x+(1-\\alpha)y)=\\alpha Ax+(1-\\alpha)Ay=\\alpha b+(1-\\alpha)b=b$ ）
不等式的所有解 $Ax\\leq b$ （通过凸集的定义证明）

凸函数

凸函数定义：函数f的定义域为凸集，对于定义域里的任意x, y，函数满足： $f(θx+(1?θ)y)≤θf(x)+(1?θ)f(y)$

凸函数理解：同样通过定义和函数图像两方面进行理解，从函数定义可知，对于函数中的任意两点x,y，需要满足 $f(θx+(1?θ)y)≤θf(x)+(1?θ)f(y)$ ；从函数图像角度理解，就是对于x,y两点之间任意点（ $θx+(1?θ)y$ 上的任意一个点）对应的函数值 $f(θx+(1?θ)y)$ 都要低于f(x)和f(y)连线 $θf(x)+(1?θ)f(y)$ 上的对应值。如下图所示：

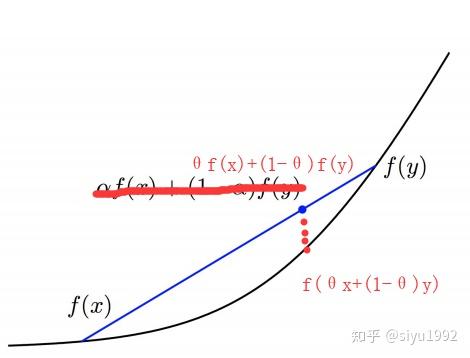
凸函数与凹函数之间的关系：如果f(x)是凸函数，则-f(x)是凹函数

凸函数的证明方法（函数定义域为凸集的前提下）：

通过凸函数的定义，证明 $f(θx+(1?θ)y)≤θf(x)+(1?θ)f(y)$
first order covexity conditions：假设 $f : R^{n}\\rightarrow R$ 是可导的(differentiable), 则f为凸函数，当且仅当 $f(y) ≥ f(x) + ?f(x)^T (y ? x)$ （不常用）
second order covexity conditions：假设 $f : R^{n}\\rightarrow R$ 是二次可导的(twice differentiable)，则f为凸函数，当且仅当 $?2 f(x) \\succeq 0$ （常用）

常见凸函数及证明：

逻辑回归目标函数（交叉熵损失函数）：具体函数见上节（由方法3证明， $\\frac{\\partial^2 \\mathcal{L}}{\\partial^2 \\mathbf{w}}=\\sum_{i=1}^{n}\\sigma({w}^{T}{x}^{(i)}+{b})*[1-\\sigma({w}^{T}{x}^{(i)}+{b})]*x^{(i)}[x{(i)}]^{T}$ 是交叉熵损失函数的2阶导数， $\\sigma()$ 函数的值域是(0,1)，因此连乘的3个式子都是大于0的，因此整体式子大于0）
二次方函数(quadratic function)： $f(x)=\\frac{1}{2}x^{T}Ax + b^{T}x + c$ ，对于任意 $A\\succeq0$ (符号解释： $\\succeq$ 是正定符号，说明矩阵A是正定矩阵，满足条件：针对任意x， $x^{T}Ax\\geq0$ )（由方法3证明： $\\frac{\\partial \\mathcal{f(x)}}{\\partial\\mathbf{x}}=\\frac{1}{2}(A+A^{T})x+b=Ax+b$ ， $\\frac{\\partial^2 \\mathcal{f(x)}}{\\partial^2\\mathbf{x}}=A$ , $A\\succeq0$ ）

维基百科中罗列了一些经典的凸优化问题和对应的维基百科链接，在此总结一下：

Least squares（最小二乘法，常用，目标：线性关系；限制条件：线性关系）
Convex quadratic minimization with linear constraints（线性约束条件下的二次规划问题，常用，目标：平方关系；限制条件：线性关系）
Linear programming（线性规划）
Quadratic minimization with convex quadratic constraints
Conic optimization
Geometric programming
Second order cone programming
Semidefinite programming
Entropy maximization with appropriate constraints

在实际的业务应用场景中，我们定义出的目标函数很可能是非凸函数，非凸函数不仅可能存在很多局部最优解，对我们寻找全局最优解造成了很大的困扰，甚至有些优化方法论的复杂度非常高，可能是 $O(p^N)$ 这样的NP hard问题，这样的问题我们是没有办法很好进行优化的，因此我们在寻找优化方法论时，一定要选择更合理的方法论。很多非凸优化问题可以转化（并非是等价的）为凸优化问题，并给出问题的近似解。

松弛（Relaxation）

通过对问题限制条件的松弛，可以将原问题等价为凸优化问题。注：松弛原问题，只能得到一个可行域更大的问题，如果原问题是求最小，则松弛后的问题的最优值一定小于等于原问题的最优值，这也是一种给出下界的方法。松弛不仅仅用于整数约束，只要利于将定义域非凸变为凸集即可。

说起来可能比较抽象，我们通过下面的Set cover Problem来详细说明一下

Set cover Problem

问题定义：假设集合U={1,2,3,4,5}，集合S={ $S_1$ ={1,2}, $S_2$ ={3}, $S_3$ ={1,2,3}, $S_4$ ={4}, $S_5$ ={5}, $S_6$ ={4,5}}，找出集合S中最少的子集，使其并集属于集合U

问题分析：尝试罗列所有满足条件的S的子集集合，使这些集合的并集属于集合U，假设每种组合子集的个数为x ，则满足条件的集合组合有：{ $S_1,S_2,S_6$ }x=3 ;{ $S_1,S_2,S_4,S_5$ }x=4 ;{ $S_3,S_6$ }x=2 ;很容易可以看出{ $S_3,S_6$ }组合是我们想要的组合，因为其中的子集个数最少

数学模型建模：罗列所有可能的S集合子集的组合，最小化子集个数。我们假设子集组合中子集的个数为x ，则该问题的目标函数为： $minimize_x \\sum_{i=1}^{n}{x_i},s.t.\\sum_{i:e\\epsilon S_i}^{}{x_i\\geq1},x_i\\epsilon$ {0,1}。s.t.限制条件的含义是，筛选出 $S_i$ 集合的个数大于等于1，且 $x_i$ 只有两个取值，1表示 $S_i$ 满足条件，0表示不满足

判断该问题是否是凸优化问题：目标函数定义域为 $x_i\\epsilon$ {0,1}，定义域就不是一个凸集，因为定义域集合是离散的点，两点连线的任何值都不属于 $x_i$ 集合，因此该目标函数不是凸函数，该优化问题也不是凸优化问题

优化方法：

从子集个数为1的组合开始，列出S集合子集的所有排列组合，找到满足问题条件的第一组组合就停止循环，这一组就是最终结果。该优化方法论是最笨的方法，但是该优化算法的复杂度是 $O(p^N)$ 的，属于NP hard类型问题，一旦S集合的子集数量大起来，根本无法解决。
Relaxation（松弛）：原问题是 $minimize_x \\sum_{i=1}^{n}{x_i},s.t.\\sum_{i:e\\epsilon S_i}^{}{x_i\\geq1},x_i\\epsilon$ {0,1}。从中我们不难发现，目标函数主体 $x_i$ 是一个线性的，条件 $x_i\\geq1$ 也是线性的，不看另一个约束条件的话，我们可以认为，这两个函数和限制条件的组合是一个LP问题（Linear Programming）；但是看 $x_i\\epsilon$ {0,1}条件呢，这个限制条件又是Integer Programminig问题，组合一下所有问题吧，可以原问题定义为Integer Linear Programming问题。对于这样类型的问题，其实没有高效的优化方法论的，因为它是一个NP complete问题。但是我们通过Relaxation的方法论，我们可以通过转换 $x_i\\epsilon$ {0,1}限制条件为 $x_i\\epsilon$ [0,1]把整个问题转换为一个Linear Programming问题，该问题是凸优化问题。因此得出的新的问题为： $minimize_x \\sum_{i=1}^{n}{x_i},s.t.\\sum_{i:e\\epsilon S_i}^{}{x_i\\geq1},x_i\\epsilon$ [0,1]

通过GD（梯度下降）的优化方法论，我们可以得出全局最优解。但是，我们的出来参数 $x_i$ 的解只是原问题的一个近似问题的解，因此，我们需要对 $x_i$ 做一个基于规则的变换，使 $x_i$ 满足 $x_i\\epsilon$ {0,1}。这里可以添加规则，如果 $x_i\\geq0.5$ , $x_i=1$ ， $x_i<0.5$ , $x_i=0$

松弛（Relaxation）的问题点

通过上面Set cover Problem中通过relaxation的方式求解参数，我们不难发现，其实通过对问题的转化，我们虽然能够快速对问题求解了，但是我们求出来的最优解与原问题的最优解可能是相等，也可能有一定的误差的，所以通过relaxation，我们需要证明relaxation得出的最优解和原问题的最优解的误差范围。

当我们拿到一个业务问题，一定需要按照算法思维那一节做，先将问题转换为一个严谨的数学问题，判断我们写出的目标函数的凹凸性，如果目标函数非凸，我们需要对问题的限制条件做一些转化，进而求出转化后问题的近似解，并证明其与原问题的误差范围。如果是凸函数，我们需要选择相应的优化方法论进行优化，因为优化问题是机器学习算法中的核心部分。

以上是对凸优化的方法论的一些总结与梳理，不得不说，凸优化是一个很深奥也很大的领域，并且通过一些非凸函数的优化方法论，也能感受出如果要严格解决一个数学问题，步骤是很严谨的，文中的观点如果有错误的地方，还请各路大神不吝赐教。

references：

返回列表

优化结构并保持合理增速，塑造中国经济长期竞争力

加拿大初中留学条件有哪些？有什么要求呢？